|
(Слайд 4) Казалось бы, что понятие числа должно возникнуть одновременно с умением считать, но это далеко не так. Замечено, что считать до пяти умеют и кошки и свиньи, но чтобы перейти от пяти предметов к числу «пять», требовалось великое открытие, и вот почему. Пять собак или пять овец – это совсем не то, что пять орехов. Ведь пять орехов – очень мало, съел – и не заметил, а пять овец – очень много, их хватит, чтобы долго кормиться большой семье. Пять собак – это стая, которая может хорошо защитить от диких зверей, а пять блох на собаке и разглядеть-то трудно. Разве можно их сравнивать?
(Слайд 5) Знаменитый русский путешественник Н. Н. Миклухо-Маклай, проведший много лет среди туземцев на островах Тихого океана, обнаружил, что у некоторых племён имеется три способа счёта: для людей, для животных и для утвари, оружия и прочих неодушевлённых предметов. То есть там в то время ещё не появилось понятие числа, не было осознано, что три ореха, три овцы и три ребёнка обладают общим свойством – их количество равно трём.
Итак, появились числа 1, 2, 3, …, которыми можно выразить количество коров в стаде, деревьев в саду, волос на голове. Эти числа в последствии получили название натуральных.
(Слайд 6) Гораздо позднее появился ноль, которым обозначали отсутствие рассматриваемых предметов.
Вы, конечно, неоднократно слышали о достижениях математиков Древней Греции. Они поистине великолепны и вызывают невольное восхищение. Но одного открытия древние греки не сделали. Они не придумали ноля. Нам легко с высоты многовекового опыта человечества удивляться этому факту! А это было совсем не просто. Что такое «ничего»? Пустое место! Если ничего нет, кому придёт в голову что-то писать, когда можно не писать ничего!
Кто первым догадался обозначить цифрой «ничто»? Мы никогда не узнаем. Можем только утверждать, что таких гениев было несколько. Кто-то придумал знак для нуля в Древнем Вавилоне. Кто-то из индейцев майя – в Америке. Кто-то – в Китае. И кто-то из мудрецов Индостана обозначил пустое место тем самым кружком, которым весь мир пользуется до сих пор.
Итак, началась славная жизнь ноля – цифры и числа.
Ноль-цифра дал возможность не выдумывать новых знаков для больших чисел. Теперь любое число можно было записать, используя одни и те же цифры, и уже не спутаешь 12 со 120 или 102 – если в каком-то числе есть сотни и единицы, но нет десятков, в отведенном для десятков месте достаточно написать, что их – ноль. Появилась позиционная система счисления, в которой значение цифры зависит от ее места в числе – позиции.
(Слайд 7) Ноль-число и сам по себе весьма примечателен. К какому числу его ни прибавь, оно не изменится (ведь мы прибавили «ничего»). На какое число его ни умножь, будет снова ноль (мы взяли число ноль раз, т.е. ни разу). Сам он делится на любое число (пустое место как ни дели – все равно ничего не будет). Зато делить на него самого нельзя: разве можно что-то разделить на ноль частей? Если бы это удалось, как из нуля частей сложить вновь то, что мы разделили? Чтобы избежать этой неприятности, деление на ноль пришлось запретить.
(Слайд 8) Ноль – удобное обозначение начала пути. Если вы едете по шоссе, мимо вас мелькают километровые столбы: 10 км, 11 км, 12 км... от чего? От главного почтамта того города, откуда вы выехали.
(Щелчок) Ноль – начало всех времен... Только где это начало? Может быть это момент возникновения Вселенной? Но если такой момент и был, то очень давно, и точно сказать, сколько лет прошло с тех пор, никто не сможет – разве что примерно, с точностью до миллиардов лет. А считать годы нужно. Но раз неизвестно, когда состоялось «сотворение мира», почему не поступить так же, как и с расстояниями? Выберем какое-нибудь знаменательное событие, скажем, что оно произошло в нулевой момент времени, и от него пойдет первый год. (Щелчок) Так мы и делаем: говорим, что первый год нашей эры начался с Рождества Христова, а всё, что было до того – было до нашей эры.
(Слайд 9) Однако торговцам и ремесленникам натуральных чисел и ноля было мало, поскольку возникали задачи деления на части земли, наследства и многого другого. Так появились дроби и правила обращения с ними.
(Щелчок) Первой дробью, с которой познакомились люди, была половина. (Щелчок) Следующей дробью была треть. (Щелчок) Таким образом, первые дроби, с которыми нас знакомит история, это дроби вида – 1/2, 1/3, 1/4 …– так называемые единичные дроби.
Единичные дроби встречаются в древнейших дошедших до нас математических текстах, составленных более 5000 лет тому назад, – древнеегипетских папирусах и вавилонских клинописных табличках.
(Щелчок) Египтяне все дроби старались записать как суммы единичных дробей. Например, вместо 8/15 они писали1/3 + 1/5. Дробь 7/8 записывали в виде долей: 1/2 + 1/4 + 1/8. Производить арифметические действия над числами, всякий раз раскладывая их в сумму долей единицы, очень неудобно, но есть и некоторое преимущество.
(Слайд 10) Рассмотрим такую задачу: «Разделить 7 хлебов между 8 людьми».
Очевидно, каждый должен получить 7/8 одного хлеба. Современный школьник, скорее всего, решал бы задачу так: надо разрезать каждый хлеб на 8 равных частей и каждому человеку дать по одной части от каждого хлеба. А вот как эта задача решена на папирусе Райнда – это древнеегипетский математический текст.
Поскольку 7/8 = 1/2 +1/4 +1/8. Следовательно, каждому человеку нужно дать по половине, четверти и восьмушке хлеба. Теперь ясно, что надо 4 хлеба разрезать пополам, 2 хлеба на 4 части и только один хлеб – на 8 частей. И если нашему школьнику пришлось бы сделать 49 разрезов, то решая задачу через единичные дроби – всего 17, т.е. египетский способ почти в 3 раза экономичнее.
Для разложения неединичных дробей на сумму единичных существовали готовые таблицы, которыми и пользовались египетские писцы для необходимых вычислений.
(Слайд 11) В древности наибольшего развития обыкновенные дроби достигли в Индии. В рукописях, относящихся к 4 веку до нашей эры, встречаются уже не только единичные дроби, но и дроби с произвольными числителями.
В начале VII столетия индийцы знали и формулировали правила действий над обыкновенными дробями. Складывать, умножать и делить дроби, записанные в виде обыкновенных дробей, достаточно сложно. Куда проще обращаться с десятичными дробями. Во-первых, чтобы складывать, вычитать или перемножать такие дроби, не нужно никаких специальных правил вроде столь мучительного поиска общего знаменателя. Во-вторых, сделать из обыкновенной дроби десятичную ничего не стоит – дели себе числитель на знаменатель, пока не разделится без остатка.
Вот тут-то и подстерегает неприятность! Подавляющее число таких делений не заканчивается никогда! Если делить, скажем, десять на три, мы будем снова и снова получать все ту же тройку...
Но практическим нуждам все эти тонкости совершенно не мешают. Разумеется, в жизни просто округляют бесконечную десятичную дробь до конечной, а дальше с ней легко работать...
(Слайд 12) Появились десятичные дроби в трудах арабских математиков в средние века и независимо от них – в древнем Китае. Но и раньше, в древнем Вавилоне, использовали дроби такого же типа, но шестидесятеричные. В европейскую же практику десятичные дроби ввел Симон Стевин. До тех пор каждый, кто сталкивался с нецелыми числами, должен был возиться с числителями и знаменателями...
Вернемся к истории. (Щелчок) С появлением дробей торговцам и ремесленникам чисел было уже достаточно.
(Слайд 13) Кстати, если ко множеству целых чисел присоединить все дробные числа, то получится множество рациональных чисел (от лат. ratio – отношение). Таким образом, рациональные числа – это числа, представимые в виде отношения, т.е. обыкновенной дроби.
(Слайд 14) Но ещё математики Древней Греции, ученики знаменитого Пифагора, обнаружили, что есть числа, которые не выражаются никакой дробью. Первым таким числом стала длина диагонали квадрата, сторона которого равна единице. Это так поразило пифагорейцев, что они решили скрыть этот факт от всех. Но, как это часто бывает со всякого рода тайнами, нашелся некто Гиппас, который все же не удержался и, как мы сказали бы теперь, разгласил запретную информацию. Легенда утверждает, что боги наказали его – он утонул во время кораблекрушения. Новые числа стали называть иррациональными – значит не выражающиеся в виде отношения.
(Слайд 15) На этом история числа не кончилась. Рассмотрим историю появления отрицательных чисел.
Во 2 веке до нашей эры китайский учёный Чжан Цань написал книгу «Математика в девяти главах». В этой книге впервые в науке встречаются отрицательные числа. Полного и ясного понимания природы отрицательных чисел и правил действий над ними у автора не было. Каждое отрицательное число он понимал как долг, а положительное – как имущество.
Знак минус тогда не знали, и, чтобы отличить числа, выражающие долг, Чжан Цань писал их другими чернилами, чем числа, выражающие имущество (положительные).
Хотя китайские учёные и объясняли отрицательные числа как долг, всё же они избегали употребления их и стремились заменять условие задачи, чтобы в итоге получилось решение положительное. Как не старались учёные избегать отрицательных чисел, называя их «абсурдными», «ложными», а жизнь ставила перед наукой новые и новые задачи, и всё чаще и чаще задачи эти приводили к отрицательным числам и в Китае, и в Индии, и в Европе.
В 7 веке индийский математик Брахмагупта (около 598 – 660 гг.) правильно производил действия сложения и вычитания отрицательных чисел. Правила умножения и деления положительных и отрицательных чисел впервые появляются у индийского математика 12 века Бхаскары.
Независимо от индийцев итальянский математик Леонардо Фибоначчи в 12 веке также пришёл к мыслям, что отрицательные числа надо понимать в смысле, противоположном положительным.
В 17 веке великий французский учёный Рене Декарт предложил откладывать отрицательные числа на координатной оси влево от нуля. Нам сейчас кажется это таким простым и понятным, но, чтобы дойти до этой мысли, потребовалось восемнадцать веков работы учёной мысли от китайского учёного Чжан Цаня до Декарта.
(Слайд 16) Итак, математики ввели отрицательные числа, которые оказались очень удобными при решении многих задач. Казалось бы, уже всё, но в ряде случаев возникает потребность найти число, квадрат которого равен минус единице. Среди известных чисел такого не оказалось, поэтому его обозначили буквой i и назвали мнимой единицей. Числа, полученные умножением ранее известных чисел на мнимую единицу, например, 2i или 3i/4, слали называть мнимыми, в отличие от существовавших, которые стали называть действительными или вещественными, а сумму действительных и мнимых чисел, такие как 5 + 3i, стали называть комплексными числами.
Сначала многие математики не признавали комплексных чисел, пока не убедились в том, что с их помощью можно решать многие технические задачи, которые до этого не поддавались решению. Так, с их помощью русский математик и механик Николай Егорович Жуковский создал теорию падения, показал, как можно рассчитывать подъёмную силу, возникающую при обтекании воздухом крыла самолёта.
(Слайд 17) В настоящее время существует следующая классификация чисел. Натуральные числа, им противоположные отрицательные числа и ноль составляют множество целых чисел. Целые числа и дробные (обыкновенные и десятичные дроби) образуют множество рациональных чисел. Рациональные числа и иррациональные числа составляют множество действительных чисел. А уже множества действительных и мнимых чисел образуют множество комплексных чисел.
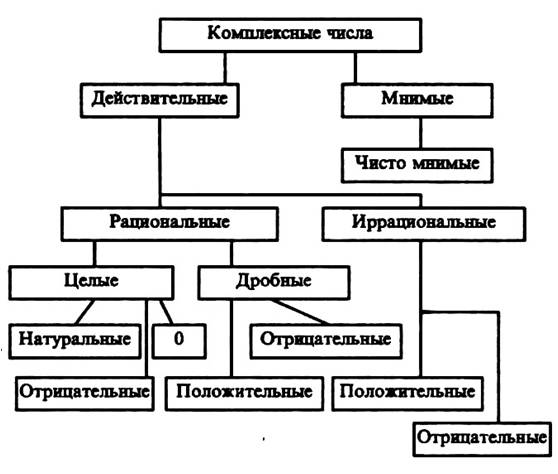
Кто знает, может быть в скором времени возникнет необходимость в существовании ещё каких-нибудь чисел. Поэтому утверждать, что представленная схема является окончательной нельзя.
(Слайд 18) История числа продолжается…
|





